“规划求解”是一组命令的组成部分，这些命令有时也称作假设分析工具。借助“规划求解”，可求得工作表上某个单元格（被称为目标单元格）中公式的最优值。“规划求解”将对直接或间接与目标单元格中公式相关联的一组单元格中的数值进行调整，最终在目标单元格公式中求得期望的结果。“规划求解”通过调整所指定的可更改的单元格（可变单元格）中的值，从目标单元格公式中求得所需的结果。在创建模型过程中，可以对“规划求解”模型中的可变单元格数值应用约束条件，而且约束条件可以引用其他影响目标单元格公式的单元格。

使用“规划求解”可通过更改其他单元格来确定某个单元格的最大值或最小值。例如，您可更改计划广告预算额来查看对您的计划收益额的影响。

“规划求解”示例

在下面的示例中，每个季度的“广告费”直接影响到“销售数量”，从而间接决定了销售收入以及相关的成本和利润。通过“规划求解”可以更改季度广告费用（在单元格区域 B5:E5 中），以使总利润达到最大值。其中，总预算不能超过 $20,000（在单元格 F5 中）。可变单元格中的数值用来计算每个季度的利润，所以它们与目标单元格 F7 中的公式 =SUM(一季度利润:二季度利润)相关联。

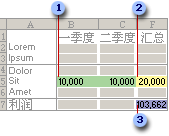
可变单元格

约束条件单元格

目标单元格

运行“规划求解”后得到的新数值如下：

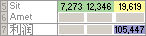
“规划求解”示例工作表

Microsoft Excel 在 Office\Samples 文件夹下有一个工作簿 (Solvsamp.xls)，其中给出了可以解决的问题类型的示例。

您可以借助 Solvsamp.xls 中的示例工作表来解决一些实际问题。一共有六张工作表可用：“产品组合”、“货物传送”、“排班组合”、“最大收益”、“投资方案”和“电路设计”。若要使用某个示例工作表，请打开工作簿，切换到相应工作表，再单击“工具”菜单中的“规划求解”。示例工作表中的目标单元格、可变单元格和约束条件已经被指定了。

“规划求解”算法与方法

Microsoft Excel 的“规划求解”工具取自德克萨斯大学奥斯汀分校的 Leon Lasdon 和克里夫兰州立大学的 Allan Waren 共同开发的 Generalized Reduced Gradient (GRG2) 非线性最优化代码。

线性和整数规划问题取自 Frontline Systems 公司的 John Watson 和 Dan Fylstra 提供的有界变量单纯形法和分支边界法。有关“规划求解”使用的内部求解过程的详细信息，请与下列地址联系：

Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
网站：http://www.frontsys.com
电子邮件：info@frontsys.com

Microsoft Excel Solver 程序代码的部分为 Frontline Systems, Inc 1990、1991、1992 和 1995 年版权所有，部分为 Optimal Methods, Inc 公司 1989 年版权所有。